7,692
17
0
Ikke bruk mobilkalkis til skatteberegning!
22,342
Akershus
0
Merkelig, og ikke bare på denne mobilen. Prøv selv. Bytt rekkefølgen også.
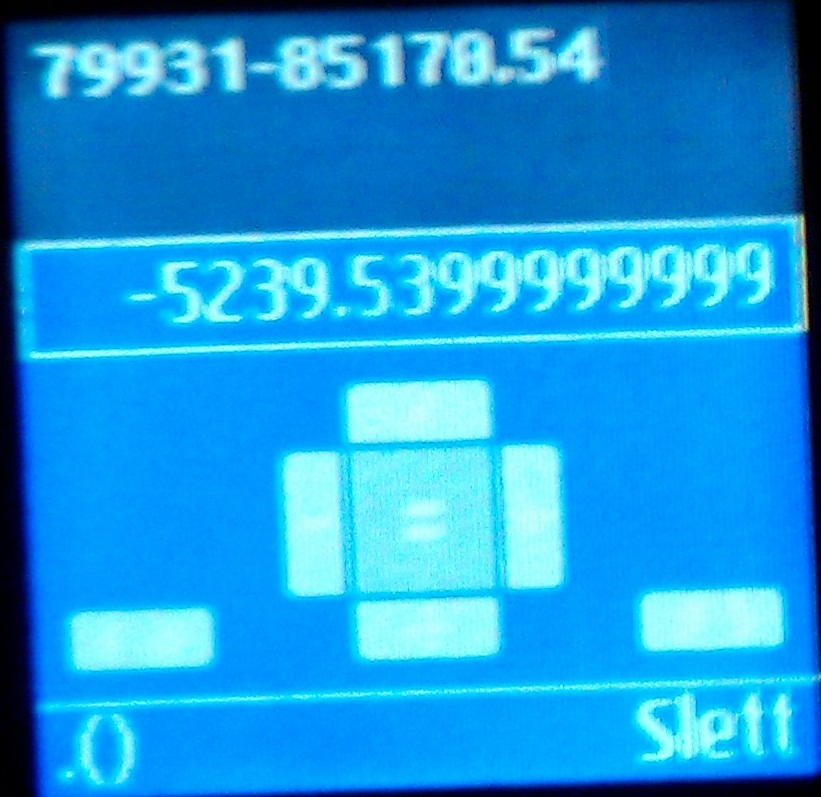
Dette var på en Samsung, men får samme svaret på en HTC også.
God 16,9999999 mai ;D
Det er fordi beregningene er gjort med flyttall. Det er bare lite elegant, forskjellen på 16,999999999999 og 17 har ingen ting å si i praksis. Det er et velkjent problem innen dataverdenen, absolutt nøyaktighet har man kun når man regner med heltall. Det er smådårlig programmering, men ikke nødvendigvis "feil". Når man regner med flyttall så har man en gitt presisjon - typisk svært mange desimaler etter komma, men av brukerhensyn rundes det gjerne av i brukergrensesnitett slik at det ser penere ut. Man forventer selvsagt at svaret her skal bli -5239.54, det er ikke det, men om du fyller inn uendelig mange nitall etter 3-tallet du får i svaret så er det i praksis det samme. Når hadde du sist behov for å regne med signifikant sjettedesimal eller 31. desimal?
Ift tittelen - hvorfor kan man ikke bruke en mobilkalkis til skatteberegning? Presisjonsnivået i norske kroner er 0.01 krone, kalkulatoren det er snakk om her regner betydelig mer nøyaktig enn det.
Jeg synes bare dette virker kjipt.
Hvorfor gir subtraksjon mellom 2 hele tall en differanse som må rundes av?
Er ikke -5239,54 et bedre svar enn trådstarter sitt avrunda tall?
Selvsagt.
Den interesserte kan lese om flyttallsproblematikk her
http://en.wikipedia.org/wiki/Floating_point#Accuracy_problems
Selv om det i praksis blir samme svaret.
Til skatteberegning fungerer den nok, selv om den er litt teit.
Men når du gjør styrkeberegninger på en 600 meters høy bygning, kan denne regnefeilen begynne å få litt å bety.
Nei.
Det er alt for mange andre faktorer som er avrundet, tilnærma og ikke nøyaktige av andre grunner til at denne flyttallsunøyaktigheten får noko som helst innflytelse.
Excel har akkurat samme problem: =1,324 - 1,319 gir svaret: 0,00500000000000012
Flyttall har akkurat samme mengde signifikante siffer om ein reknar på 1000000000 eller på 0,0000000000001 og nøyaktigheten i utrekningane blir den samme.
Ein må berre passe på når ein konverter til heiltall eller andre talltyper med faste antall desimaler at ein ikkje får slike utslag som vist her.